完全解读布隆过滤器
此章节是黑马点评 Plus 版本中专有的内容,而在整套文档中将普通版本和 Plus 版本都融合在了一起,让大家更方便的学习。
布隆过滤器(Bloom Filter)是 1970 年由布隆提出的,是一种非常节省空间的概率数据结构,运行速度快,占用内存小。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。主要用于判断一个元素是否在一个集合中。主要是解决大规模数据下不需要精确过滤的场景,如检查垃圾邮件地址,爬虫URL地址去重,解决缓存穿透问题等。
优点
- 存储空间和插入 / 查询时间都是常数O(k)
- 支持海量数据场景下高效率判断元素是否存在
- 存储空间小,不存储数据本身,而是存储hash结果取模运算后的位标记
缺点
- 无法删除,因为可能多个元素通过哈希后,可能会产生hash碰撞,映射到布隆过滤器的同一个位置。删除该位置后,可能影响其他元素
- 误判,由于存在hash碰撞,不同的元素经过哈希后可能映射到同一个位置,一旦产生碰撞,会被误判存在
- 碰撞概率,让随着元素越来越大,在容量限制下,布隆过滤器被使用的位置就会越来越多,误判的几率也会越来越大
特点
根据布隆过滤器的特点可以知道:
- 判断如果某个元素存在,由于存在误判,这个元素不一定是存在的
- 判断如果某个元素不存在,那这个元素一定不存在
原理
结构
布隆过滤器底层就是一个二进制的位数组,在初始状态,所有位置的位都是0
添加
- 使用哈希函数对元素进行哈希计算得到索引值,将索引值对应的数组下标所在的值设置为1
- 如果是多个哈希函数则进行上述同样的操作
查询
- 对要查询的元素同样使用哈希函数进行计算,如果存在多个哈希函数则得到多个索引值
- 判断这些索引值对应的数组下标的值是否都为1,如果是,则判断这个元素为存在。如果这些下标的值只要有一个是0,那么判断这个元素为不存在
流程图
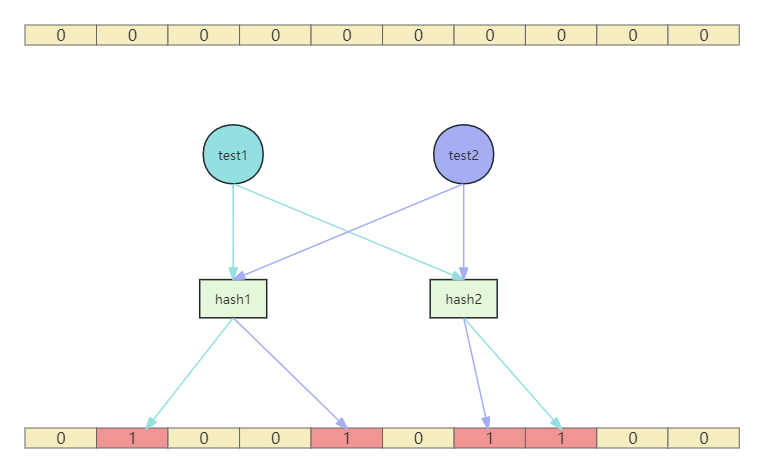
容量估算
当我们知道了布隆过滤器的原理后,还剩下个问题,就是要估算出布隆过滤器所需要的容量,以便于配置服务器的容量
布隆过滤器的容量是和产生的碰撞概率有关的,通过布隆过滤器的原理能知道,容量和碰撞概率的关系就是相斥的
要想碰撞概率小,容量肯定就要大。
要想容量小,碰撞概率肯定就要大
公式
那么具体要如何估算呢,我们可以根据公式要进行计算:
m = -(n × ln p) / (ln 2)^2
m可能算到小数,那就向上取整
参数解释
n元素的样本量p碰撞率m布隆过滤器占用比特数
进行计算
以用户注册业务为例,我们需要计算 n,也就是用户量需要多少
2023年末2024年初,常住人口140967万人,这里我们直接取整为14亿,假设这14亿人所有人都是大麦网的用户,用这个数字作为布隆过滤器的容量来说,以目前国内的用户增长量来说,五年内绝对是没有任何问题的
至于碰撞率 p 我们取一个比较精确的值,0.2%
将n = 14亿 ,p = 0.2% 带入公式中,计算出
m ≈ 1.8108849535 × 10^10
这时 m 的单位是bit,如果换成GB单位, 则
m ≈ 2.108 GB
布隆过滤器组件
讲解完布隆过滤器后,下面就是开始使用了,在经典的开源项目 **Redisson,**项目中提供了布隆过滤器的支持,如果小伙伴对 Redisson 感兴趣,可跳转到对应的地址
本人将 Redisson 的布隆过滤器集成到项目中了,使用起来更加简单
依赖
<dependency>
<groupId>org.javaup</groupId>
<artifactId>hmdp-bloom-filter-framework</artifactId>
<version>${revision}</version>
</dependency>
关于项目中布隆过滤器组件的详细设计讲解,可跳转到: